CF232C Doe Graphs

John Doe 决定必须用他的名字来命名某个数学对象。于是他发明了 Doe 图。Doe 图是一类无向图，每一个都由一个非负整数（其阶数）唯一决定。 我们用 $ D(k) $ 表示阶数为 $ k $ 的 Doe 图，用 $ |D(k)| $ 表示 $ D(k) $ 中的顶点数。那么 Doe 图的定义如下： - $ D(0) $ 只包含一个编号为 $ 1 $ 的顶点。 - $ D(1) $ 包含两个编号为 $ 1 $ 和 $ 2 $ 的顶点，这两个顶点之间有一条边相连。 - 当 $ n \geq 2 $ 时，$ D(n) $ 由 $ D(n-1) $ 和 $ D(n-2) $ 得到。将 $ D(n-1) $ 与 $ D(n-2) $ 合并为同一个图，其中 $ D(n-2) $ 的全部顶点编号增加 $ |D(n-1)| $（例如，原本 $ D(n-2) $ 的顶点 $ 1 $ 变为 $ 1+|D(n-1)| $）。然后添加两条边：第一条连接 $ |D(n-1)| $ 和 $ |D(n-1)|+1 $，第二条连接 $ |D(n-1)|+1 $ 和 $ 1 $。注意，根据定义，$ D(n) $ 是连通图，其顶点编号为 $ 1 $ 到 $ |D(n)| $。 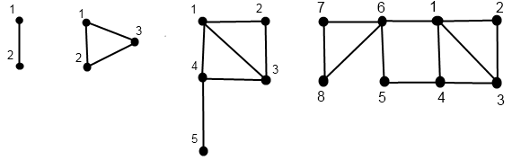 图中依次从左到右分别是 Doe 图的阶数 1、2、3、4。 John 认为 Doe 图非常优秀，因为存在一种多项式时间算法能够在 Doe 图上寻找哈密顿路径。然而，你的任务是回答多个关于在 $ D(n) $ 中查询指定顶点 $ a_{i} $ 和 $ b_{i} $ 间的最短路径长度的问题。 在图中，顶点 $ u $ 和顶点 $ v $ 之间的一条路径是一个顶点序列 $ x_{1}, x_{2}, \dots, x_{k} $ （$ k>1 $），使得 $ x_{1}=u $，$ x_{k}=v $，并且对于任意 $ i $（$ i

第一行包含两个整数 $ t $ 和 $ n $（$ 1 \leq t \leq 10^{5}；1 \leq n \leq 10^{3} $），分别表示查询的数量和给定 Doe 图的阶数。接下来的 $ t $ 行，第 $ i $ 行包含两个整数 $ a_{i} $ 和 $ b_{i} $（$ 1 \leq a_{i}, b_{i} \leq 10^{16} $，$ a_{i} \neq b_{i} $），表示第 $ i $ 个询问的两个顶点编号。保证 $ a_{i}, b_{i} \leq |D(n)| $。 请注意，在 C++ 中读入或输出 64 位整数时，不要使用 %lld，而应优先使用 cin、cout 流或者 %I64d 格式。

对于每个查询，输出一行一个整数，表示顶点 $ a_{i} $ 和 $ b_{i} $ 之间最短路径的长度。输出顺序与输入顺序一致。

由 ChatGPT 5 翻译