CF268D Wall Bars

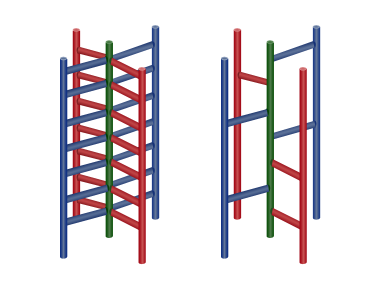
Manao 正在一家建筑公司工作。最近这家公司要在一个儿童公园建造墙杆。Manao 受委托制定一项建造计划。 Manao 的正确设计描述如下： - 建筑中心是一根高度为 $n$ 的主杆。 - 在高度 $1, 2, ..., n$ 处，正好有一根水平横杠从主杆上伸出。每根横杠都会向四个方向中的一个方向突出。 - 孩子可以从一根栏杆爬到另一根横杠，当且仅当它们之间的高度差不超过 $h$，并且它们突出在同一个方向。如果一个孩子在地上，他可以在 $1$ 到 $h$ 之间的高度爬到任何一个横杠上。在 Manao 的设计中，一个孩子应该能够在高度 $n - h + 1, n - h + 2, ..., n$ 爬到至少一个横杠，并且他从地面开始爬。  上图是一个建造示例。 Manao 想知道，有多少种建筑满足要求？由于答案可能非常大，**所以对 $10^9 + 9$ 取模**。如果有这样的高度 $i$，则两种设计被认为是不同的，即这些设计中高度 $i$ 上的横杠不会朝同一方向突出。

一行包括两个整数 $n, h(1 \le n \le 1000, 1 \le h \le \min(n, 30))$。

一个数，即答案（对 $10^9 + 9$ 取模）。

Consider several designs for $ h=2 $ . A design with the first bar sticked out in direction $ d_{1} $ , the second — in direction $ d_{2} $ and so on ( $ 1