CF268D Wall Bars

Manao is working for a construction company. Recently, an order came to build wall bars in a children's park. Manao was commissioned to develop a plan of construction, which will enable the company to save the most money. After reviewing the formal specifications for the wall bars, Manao discovered a number of controversial requirements and decided to treat them to the company's advantage. His resulting design can be described as follows: - Let's introduce some unit of length. The construction center is a pole of height $ n $ . - At heights $ 1,2,...,n $ exactly one horizontal bar sticks out from the pole. Each bar sticks in one of four pre-fixed directions. - A child can move from one bar to another if the distance between them does not exceed $ h $ and they stick in the same direction. If a child is on the ground, he can climb onto any of the bars at height between $ 1 $ and $ h $ . In Manao's construction a child should be able to reach at least one of the bars at heights $ n-h+1,n-h+2,...,n $ if he begins at the ground. 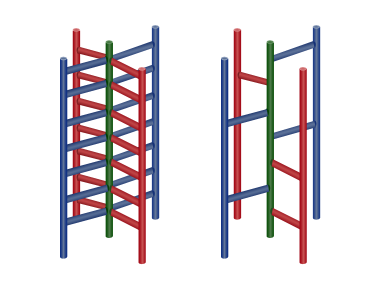The figure to the left shows what a common set of wall bars looks like. The figure to the right shows Manao's constructionManao is wondering how many distinct construction designs that satisfy his requirements exist. As this number can be rather large, print the remainder after dividing it by $ 1000000009 (10^{9}+9) $ . Two designs are considered distinct if there is such height $ i $ , that the bars on the height $ i $ in these designs don't stick out in the same direction.

A single line contains two space-separated integers, $ n $ and $ h $ ( $ 1

In a single line print the remainder after dividing the number of designs by $ 1000000009 (10^{9}+9) $ .

Consider several designs for $ h=2 $ . A design with the first bar sticked out in direction $ d_{1} $ , the second — in direction $ d_{2} $ and so on ( $ 1