CF274C The Last Hole!

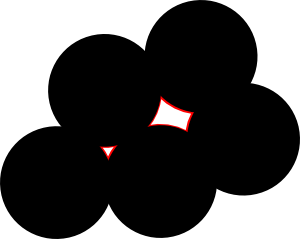
Luyi 在平面上有 $n$ 个圆。第 $i$ 个圆的圆心为 $(x_{i},y_{i})$。在时间零时刻，所有圆开始同时增长。也就是说，每个圆在时刻 $t\ (t>0)$ 的半径为 $t$。这些圆被画成黑色圆盘，分布在无穷大的白色平面上。因此，在每一时刻，平面上会出现若干个黑色和白色区域。注意，圆在增长的过程中可能相互重叠。 我们将一个“洞”定义为一个封闭且连通的白色区域。例如，下图中用红色边框标出的区域即为两个洞。在圆增长的过程中，可能会产生一些洞，并且可以很容易发现，每一个产生的洞最终都会消失。Luyi 想要你找出最后一个洞消失的时刻。换句话说，你需要找出这样一个最早时刻，使得在这之后的任何时刻都不再存在洞。 

第一行输入一个整数 $n$，表示圆的数量，满足 $1\leq n\leq 100$。接下来的 $n$ 行，每行包含两个整数 $x_{i}$ 和 $y_{i}$，表示第 $i$ 个圆心的坐标，$-10^{4}\leq x_{i},y_{i}\leq 10^{4}$。 保证任意两个圆的圆心都不在同一点。

输出最后一个洞消失的时刻。如果不可能出现洞，输出 $-1$。 如果输出为实数，则当绝对误差或相对误差不超过 $10^{-4}$ 时，均被认为是正确答案。

由 ChatGPT 5 翻译