CF280A Rectangle Puzzle

You are given two rectangles on a plane. The centers of both rectangles are located in the origin of coordinates (meaning the center of the rectangle's symmetry). The first rectangle's sides are parallel to the coordinate axes: the length of the side that is parallel to the $ Ox $ axis, equals $ w $ , the length of the side that is parallel to the $ Oy $ axis, equals $ h $ . The second rectangle can be obtained by rotating the first rectangle relative to the origin of coordinates by angle $ α $ . 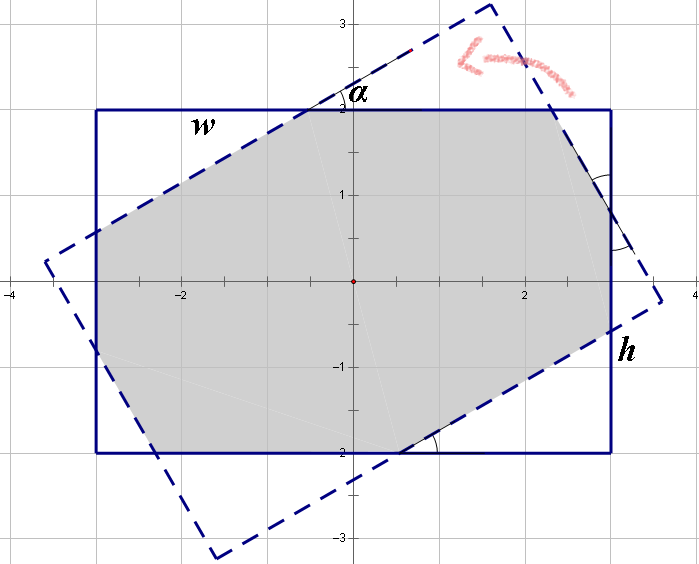Your task is to find the area of the region which belongs to both given rectangles. This region is shaded in the picture.

The first line contains three integers $ w,h,α $ $ (1

In a single line print a real number — the area of the region which belongs to both given rectangles. The answer will be considered correct if its relative or absolute error doesn't exceed $ 10^{-6} $ .

The second sample has been drawn on the picture above.