CF280B Maximum Xor Secondary

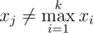Bike 喜欢在序列中寻找次大元素。对于由不同数字组成的序列 $x_{1},x_{2},...,x_{k}$（$k>1$），次大元素 $x_{j}$ 满足如下不等式： 。 给定序列 $x_{1},x_{2},...,x_{k}$（所有元素互不相同的正整数，$k>1$），序列的幸运数指的是最大元素与次大元素按位异或的结果。 现在给你一个由 $n$ 个互不相同的正整数 $s_{1},s_{2},...,s_{n}$ 组成的序列（$n>1$）。我们用 $s[l..r]$ 表示以 $l$ 到 $r$ 为端点的子区间（$1 \leq l < r \leq n$）。你的任务是求所有 $s[l..r]$ 的幸运数中的最大值。 注意，因为 $s$ 中所有数字都互不相同，所有定义均有意义。

第一行包含一个整数 $n$（$1 < n \leq 10^5$）。 第二行包含 $n$ 个互不相同的正整数 $s_{1},s_{2},...,s_{n}$（$1 \leq s_{i} \leq 10^9$）。

输出一个整数，表示所有子区间 $s[l..r]$ 的幸运数的最大值。

对于第一个样例，你可以选择 $s[4..5]=\{4,3\}$，此时幸运数为 $4 \operatorname{xor} 3 = 7$。你也可以选择 $s[1..2]$。 对于第二个样例，你必须选择 $s[2..5]=\{8,3,5,7\}$。 由 ChatGPT 5 翻译