CF285E Positions in Permutations
题目描述
排列 $p$ 是一个有序整数集 $p_{1},p_{2},\dots,p_{n}$,由 $n$ 个互不相同的正整数构成,并且每个整数都不超过 $n$。我们称排列 $p$ 的第 $i$ 个元素为 $p_{i}$。我们把数 $n$ 称为排列 $p_{1},p_{2},\dots,p_{n}$ 的大小或长度。
在排列 $p_{1},p_{2},\dots,p_{n}$ 中,若位置 $i$($1 \leq i \leq n$)满足 $|p[i]-i|=1$,则称第 $i$ 个位置是好的。请你计算恰好有 $k$ 个好位置的长度为 $n$ 的排列的数量。请将结果对 $1000000007$($10^{9}+7$)取模后输出。
输入格式
一行,包含两个用空格分隔的整数 $n$ 和 $k$($1 \leq n \leq 1000, 0 \leq k \leq n$)。
输出格式
输出一个整数,表示恰好有 $k$ 个好位置的长度为 $n$ 的排列数量,对 $1000000007$ 取模。
说明/提示
唯一的长度为 1 的排列有 0 个好位置。
排列 $(1,2)$ 有 0 个好位置,排列 $(2,1)$ 有 2 个好位置。
长度为 3 的排列:
1. $(1,2,3)$ — 0 个好位置
2. 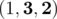 — 2 个好位置
3. 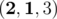 — 2 个好位置
4. 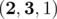 — 2 个好位置
5. 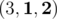 — 2 个好位置
6. $(3,2,1)$ — 0 个好位置
由 ChatGPT 5 翻译