CF286B Shifting

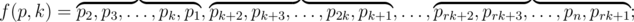
John Doe 发现了一个漂亮的排列公式。 我们设有排列 $p=p_{1},p_{2},...,p_{n}$。定义对该排列的变换 $f$ 为：  其中 $k$（$k>1$）为整数参数，$r$ 是满足 $rk \leq n$ 的最大整数。如果 $rk=n$，则 $p_{rk+1},p_{rk+2}$ 等元素将被省略。换句话说，上述排列的变换，即对每个连续长度为 $k$ 的块进行循环左移，最后一个块长度为 $n$ 除以 $k$ 的余数。 John Doe 认为 $f(f(\cdots f(p=[1,2,...,n],2)\cdots ,n-1),n)$ 这样的排列是漂亮的。不幸的是，他不能很快找到他想要的漂亮排列，因此向你求助。 你的任务是，对于给定的 $n$，找出一种漂亮的排列。详见第三个样例中的说明。

一行包含一个整数 $n$（$2\leq n\leq 10^{6}$）。

输出 $n$ 个两两不同且从 $1$ 到 $n$ 的整数，按空格分隔，表示大小为 $n$ 的漂亮排列。

关于第三组测试样例的说明： - $f([1,2,3,4],2)=[2,1,4,3]$。 - $f([2,1,4,3],3)=[1,4,2,3]$。 - $f([1,4,2,3],4)=[4,2,3,1]$。 由 ChatGPT 5 翻译