CF297A Parity Game

You are fishing with polar bears Alice and Bob. While waiting for the fish to bite, the polar bears get bored. They come up with a game. First Alice and Bob each writes a 01-string (strings that only contain character "0" and "1") $ a $ and $ b $ . Then you try to turn $ a $ into $ b $ using two types of operations: - Write $ parity(a) $ to the end of $ a $ . For example, 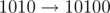. - Remove the first character of $ a $ . For example, . You cannot perform this operation if $ a $ is empty. You can use as many operations as you want. The problem is, is it possible to turn $ a $ into $ b $ ? The $ parity $ of a 01-string is $ 1 $ if there is an odd number of "1"s in the string, and $ 0 $ otherwise.

The first line contains the string $ a $ and the second line contains the string $ b $ $ (1

Print "YES" (without quotes) if it is possible to turn $ a $ into $ b $ , and "NO" (without quotes) otherwise.

In the first sample, the steps are as follows: $ 01011→1011→011→0110 $