CF297E Mystic Carvings

北极熊们在一块巨大的浮冰上发现了一些神秘的雕刻。这块冰是一个圆形的，有 $n$ 条线刻在上面。每条线连接冰面边界上的两个点（称为端点）。这些端点沿圆周逆时针编号为 $1,2,\dots,2n$。任何两条线不会共用同一个端点。 现在，有 6 只北极熊（Alice、Bob、Carol、Dave、Eve、Frank）要在这些端点上建造洞穴，每只北极熊建一个洞穴并居住其中。任意两个北极熊不能在同一个端点建洞穴。Alice 和 Bob 是一对迷信的恋人，他们相信这些线是外星人（或人类，对北极熊来说没什么两样）刻下的，并拥有某种神秘力量。因此，他们希望在被同一条线连接的两个端点分别建洞穴。Carol 和 Dave、Eve 和 Frank 也是同样的情况。 定义两个洞穴 $X$ 和 $Y$ 之间的距离为：从 $X$ 沿冰面边界走到 $Y$，途中经过的其他洞穴的最小数量加 1（只计有洞穴的端点，未建洞穴的端点不计）。 为了保证公平，这三对恋人之间的距离必须完全相同（即 Alice 和 Bob 之间的距离，Carol 和 Dave 之间的距离，以及 Eve 和 Frank 之间的距离必须相同）。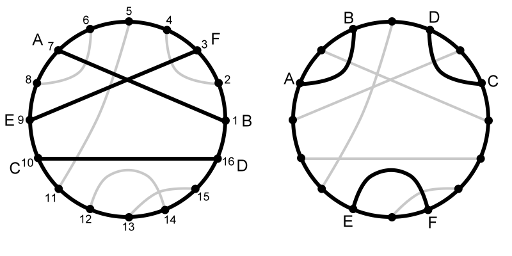 下图显示了两种不同的洞穴分布方案，圆上的点表示端点。左边的方案不合法，虽然每对恋人（A 与 B，C 与 D，E 与 F）都在同一条线的端点上，但距离要求不满足。A 与 B 之间的距离是 2（顺时针从 A 经过 F 到 B），E 与 F 之间的距离也是 2，但 C 与 D 之间的距离是 1（逆时针从 C 到 D 不经过其他洞穴）。右边的方案是合法的，三对的距离都是 1。  请计算在满足上述要求的情况下，建洞穴的方案数。若两种方案使用的 6 个端点完全相同，则认为这两种方案是同一种。

第一行包含一个整数 $n$（$3 \leq n \leq 10^5$），表示线的数量。 接下来的 $n$ 行，每行包含两个整数 $a_i,b_i$（$1 \leq a_i,b_i \leq 2n$），表示有一条线连接第 $a_i$ 和 $b_i$ 个端点。 保证每个端点恰好被一条线连接。

输出满足条件的方案数。 请不要在 C++ 中使用 `%lld`，建议使用 cin、cout 流或 `%I64d`。

第二个样例对应题目中的图片。 由 ChatGPT 5 翻译