CF298A Snow Footprints

There is a straight snowy road, divided into $ n $ blocks. The blocks are numbered from 1 to $ n $ from left to right. If one moves from the $ i $ -th block to the $ (i+1) $ -th block, he will leave a right footprint on the $ i $ -th block. Similarly, if one moves from the $ i $ -th block to the $ (i-1) $ -th block, he will leave a left footprint on the $ i $ -th block. If there already is a footprint on the $ i $ -th block, the new footprint will cover the old one. 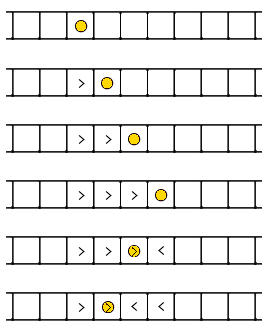At the beginning, there were no footprints. Then polar bear Alice starts from the $ s $ -th block, makes a sequence of moves and ends in the $ t $ -th block. It is known that Alice never moves outside of the road. You are given the description of Alice's footprints. Your task is to find a pair of possible values of $ s,t $ by looking at the footprints.

The first line of the input contains integer $ n $ $ (3

Print two space-separated integers — the values of $ s $ and $ t $ . If there are several possible solutions you can print any of them.

The first test sample is the one in the picture.