CF303B Rectangle Puzzle II
题目描述
给定一个矩形网格,该网格的大小为 $n\times m$。令该网格上存在一个坐标系,每个网格点都有坐标——一对整数 $(x, y)$,其中 $0 \leq x \leq n, 0 \leq y \leq m$。
你的任务是:在该网格中,找到一个最大的子矩形 $(x_1, y_1, x_2, y_2)$,使得该子矩形包含给定点 $(x, y)$,并且其长宽比恰好为 $(a, b)$。换句话说,需要满足以下条件:$0 \leq x_1 \leq x \leq x_2 \leq n$,$0 \leq y_1 \leq y \leq y_2 \leq m$,以及 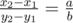。
该子矩形的边应与坐标轴平行,并且 $x_1, y_1, x_2, y_2$ 均为整数。
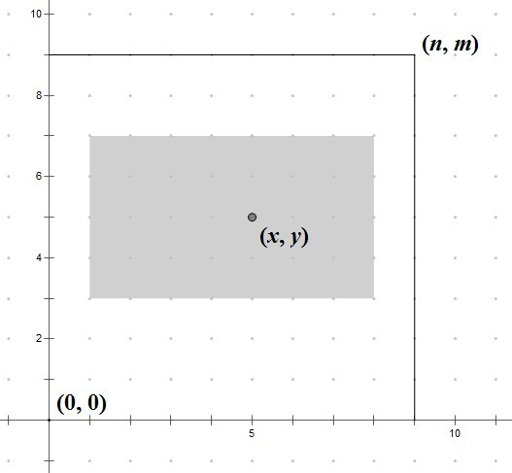 如果存在多个解,选择离 $(x, y)$ 最近的子矩形。这里的“最近”定义为 $(x, y)$ 到该子矩形中心的欧几里得距离尽可能小。如果仍然有多个解,输出字典序最小的一个。这里的字典序最小是指将子矩形视为整数序列 $(x_1, y_1, x_2, y_2)$,选取字典序最小的那个。
输入格式
第一行包含六个整数 $n, m, x, y, a, b$,满足 $1 \leq n, m \leq 10^9, 0 \leq x \leq n, 0 \leq y \leq m, 1 \leq a \leq n, 1 \leq b \leq m$。
输出格式
输出四个整数 $x_1, y_1, x_2, y_2$,表示找到的子矩形的左下角点 $(x_1, y_1)$ 和右上角点 $(x_2, y_2)$。
说明/提示
由 ChatGPT 5 翻译