CF316D1 PE Lesson

聪明的海狸决定不仅要聪明，还要做一个健康的海狸！于是他开始参加 X 学校的体育课。在这所学校里，体育老师非常有创意。他最喜欢的热身运动之一就是投球。学生们排成一排。每个人一开始都会得到一个球。球的编号从 $1$ 到 $n$（这是库存委员会的要求）。  图 1. $n=5$ 时的初始状态。学生们拿到球后开始做热身运动。这个运动包括若干次投掷。每次投掷时，老师会任意选择两个不同的学生参与。他们互相把手中的球扔给对方。这样，每次投掷后，学生们的位置不变，但这两个人手中的球会交换。 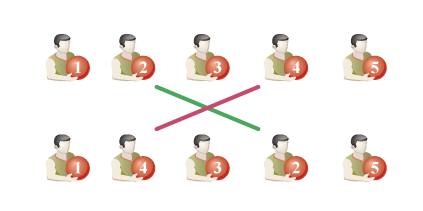 图 2. 一次投掷的示例。这次是持有第 $2$ 个球和第 $4$ 个球的学生互相投掷。由于热身运动有很多项目，每个项目的时间都很短。因此，每个学生最多只能参与有限次数的投掷。本次课中，每个学生最多参与的投掷次数为 $1$ 或 $2$。 注意，在所有投掷结束后，任何一个球都可能在任何一个学生手中。聪明的海狸决定对这个过程进行形式化，并引入了“球序列”的概念。球序列是一个长度为 $n$ 的数列，表示当前排队顺序下每个学生手中球的编号。第一个数字表示最左边学生手中的球的编号，第二个数字表示第二个学生手中的球的编号，依此类推。例如，在图 2 中，球的顺序原本是 $(1,2,3,4,5)$，投掷后变成了 $(1,4,3,2,5)$。聪明的海狸知道学生人数以及每个学生最多能参与的投掷次数。现在他想知道：在热身运动结束后，球序列可能有多少种不同的排列方式。

第一行包含一个整数 $n$，表示排队的学生数，也是球的数量。第二行包含 $n$ 个用空格分隔的整数。每个数字对应排队中的一个学生（第 $i$ 个数字表示从左数第 $i$ 个学生），表示该学生最多能参与的投掷次数。 对于 30 分的子任务（D1）： - $1 \leq n \leq 10$。 对于 70 分的子任务（D1+D2）： - $1 \leq n \leq 500$。 对于 100 分的子任务（D1+D2+D3）： - $1 \leq n \leq 1000000$。

输出一个整数，表示热身运动结束后球序列的不同排列方式总数。由于答案可能很大，请输出对 $1000000007$（$10^9+7$）取模后的结果。

由 ChatGPT 4.1 翻译