CF319A Malek Dance Club

As a tradition, every year before IOI all the members of Natalia Fan Club are invited to Malek Dance Club to have a fun night together. Malek Dance Club has $ 2^{n} $ members and coincidentally Natalia Fan Club also has $ 2^{n} $ members. Each member of MDC is assigned a unique id $ i $ from $ 0 $ to $ 2^{n}-1 $ . The same holds for each member of NFC. One of the parts of this tradition is one by one dance, where each member of MDC dances with a member of NFC. A dance pair is a pair of numbers $ (a,b) $ such that member $ a $ from MDC dances with member $ b $ from NFC. The complexity of a pairs' assignment is the number of pairs of dancing pairs $ (a,b) $ and $ (c,d) $ such that $ a<c $ and $ b>d $ . You are given a binary number of length $ n $ named $ x $ . We know that member $ i $ from MDC dances with member  from NFC. Your task is to calculate the complexity of this assignment modulo $ 1000000007 $ $ (10^{9}+7) $ . Expression 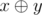 denotes applying «XOR» to numbers $ x $ and $ y $ . This operation exists in all modern programming languages, for example, in C++ and Java it denotes as «^», in Pascal — «xor».

The first line of input contains a binary number $ x $ of lenght $ n $ , $ (1

Print the complexity of the given dance assignent modulo $ 1000000007 $ $ (10^{9}+7) $ .