CF329C Graph Reconstruction
题目描述
我有一张由 $n$ 个点组成的无向图,点的编号为 $1$ 到 $n$。每个点至多有两条边与之相连。对于每一对点,至多有一条边连接它们。不存在连接自身的边。
我想构造一张新的图,使得:
- 新图包含与原图相同数量的点和边。
- 第一段中的条件依然成立。
- 对于任意两个点 $u$ 和 $v$,如果在原图中有一条边连接它们,那么在新图中就不能有这条边。
请你帮我构造出这样一张新图,或者告诉我是否不可能。
输入格式
第一行包含两个用空格分隔的整数 $n$ 和 $m$($1 \leq m \leq n \leq 10^{5}$),表示点和边的数量。接下来 $m$ 行,每行包含两个用空格分隔的整数 $u$ 和 $v$($1 \leq u, v \leq n;\ u \neq v$),表示一条连接第 $u$ 个和第 $v$ 个点的无向边。
输出格式
如果无法构造满足条件的新图,输出一行 $-1$。否则,输出恰好 $m$ 行,每行描述一条边,格式与输入一致。
说明/提示
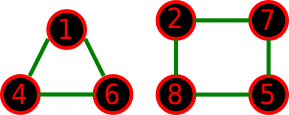
第一个样例的原图如下:

第一个样例的一种可能的新图如下:
第二个样例无法构造出任何新图。
第三个样例的原图如下:
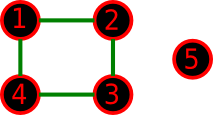
第三个样例的一种可能的新图如下:

由 ChatGPT 5 翻译