CF330B Road Construction

一个国家有 $n$ 个城市。起初，国家内没有任何道路。有一天，国王决定建设一些连接城市之间的道路。道路是双向通行的。他希望修建道路的方式能够保证：从任意一个城市出发，最多通过两条道路就可以到达其他任意一个城市。你还给出了 $m$ 对城市 —— 这些城市对之间不允许修建道路。 你的任务是修建满足上述条件的最少数量的道路。题目保证一定存在满足条件的道路分布方案。

第一行为两个整数 $n$ 和 $m$。 接下来有 $m$ 行，每行包含两个整数 $a_{i}$ 和 $b_{i}$（$1 \leq a_{i}, b_{i} \leq n$，$a_{i} \neq b_{i}$），表示城市 $a_{i}$ 和 $b_{i}$ 之间不能修建道路。城市编号为 $1$ 到 $n$。 保证每对城市最多在输入中出现一次。

第一行输出一个整数 $s$，表示需要修建的最少道路数。接下来的 $s$ 行，每行包含两个整数 $a_{i}$ 和 $b_{i}$（$1 \leq a_{i}, b_{i} \leq n$，$a_{i} \neq b_{i}$），表示应在城市 $a_{i}$ 和 $b_{i}$ 之间修建一条道路。 如果有多个答案，输出任意一个均可。

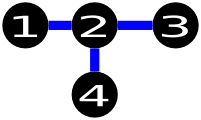
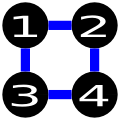
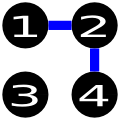
以下是样例的一个可能解法：  以下是错误解法的示例：  上面的解法错误，因为它没有使用最少的道路数（$4$ 与 $3$）。此外，它还尝试在城市 $1$ 和 $3$ 之间修建道路，但题目指定这对不能修建道路。  上面的解法错误，因为从城市 $1$ 到 $3$ 需要经过至少 $3$ 条道路，而题目要求国家内从任意城市到另一座城市最多经过 $2$ 条道路。  最后一个解法错误，因为此方案中城市 $1$ 到 $3$，$2$ 到 $3$，$4$ 到 $3$ 都无法连通。 由 ChatGPT 5 翻译