CF332D Theft of Blueprints

叛军意外获得了银河帝国需求下在一颗遥远星球建立的顶级机密研究试验场的平面图。叛军猜测该试验场正在研发新型致命武器。试验场由 $n$ 个导弹发射井组成，发射井之间通过双向地下通道相连。通道与实验室相连，实验正在这些实验室中进行。当然，通道被严密守卫：连接发射井 $i$ 和 $j$ 的通道由 $c_{i,j}$ 个战斗机器人巡逻。 叛军研究了试验场的平面图后，注意到其结构极为独特。事实证明，对于任意一个 $k$ 元素的发射井集合 $S$，恰好存在一个发射井与 $S$ 中的每一个发射井都有直接通道相连（我们称这个发射井与 $S$ 相邻）。 考虑到这一点，叛军决定按如下方式展开行动： 1. 他们选择一个 $k$ 元素的发射井集合 $S$； 2. 一组侦察兵分别空降至 $S$ 中的每个发射井； 3. 每组侦察兵沿着与 $S$ 相邻的发射井的直达通道前进（侦察兵行动时会检查各个实验室，并观察是否有武器设计图的痕迹）； 4. 在与 $S$ 相邻的发射井会合后，侦察兵乘坐飞船离开。 一次行动的危险值，是侦察兵所经过的所有通道被巡逻的战斗机器人数量之和。显然，行动的危险值只取决于如何选取集合 $S$。叛军尚未决定具体送侦察兵到哪些发射井，但他们已开始为各小队准备武器。为此，他们需要知道所有可能的 $S$ 所对应的行动危险值的数学期望。请你计算出该值，帮助叛军保卫共和国的理想！

第一行包含两个整数 $n$ 和 $k$（$2 \leq n \leq 2000$，$1 \leq k \leq n-1$），分别表示发射井的数量和侦察小队的数量。接下来的 $n-1$ 行描述试验场平面图：第 $i$ 行包含 $n-i$ 个整数 $c_{i,i+1},c_{i,i+2},...,c_{i,n}$，表示对应通道上被巡逻的战斗机器人数量（$-1 \leq c_{i,j} \leq 10^9$；若 $c_{i,j} = -1$，则 $i$ 号发射井与 $j$ 号发射井间没有通道）。所有通道为双向，即 $c_{i,j}=c_{j,i}$。不存在连接同一个发射井自身的通道。保证输入描述的平面图满足题目条件。

输出所有可能侦察行动危险值的平均数，向下取整为整数。请注意，对于给定的数据范围，答案必定可以用 64 位整型保存。 请不要在 C++ 中使用 %lld 格式输出 64 位整数，建议使用 cout 流或 %I64d 格式。

在第一个样例中，共有 6 种只包含一个元素的发射井集合。对于集合 $\{1\}$，$\{5\}$，危险值为 8；对于 $\{3\}$，$\{6\}$，危险值为 3；对于 $\{2\}$，$\{4\}$，危险值为 5。数学平均值为 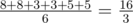。 在第二个样例中，共有 3 种只包含两个元素的发射井集合：$\{1,3\}$（危险值为 21）、$\{1,2\}$（危险值为 11）、$\{2,3\}$（危险值为 10）。平均危险值为 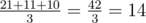。 由 ChatGPT 5 翻译