CF335C More Reclamation

在一个遥远的国度里，有两座城市分别位于一条河流的两岸。一天，这两座城市觉得自己的空间太小了，想要把一部分河流区域填成陆地。 河流区域可以用一个有 $r$ 行、恰好两列的网格表示——每个格子代表一个矩形区域。行从上到下编号为 $1$ 到 $r$，列编号为 $1$ 和 $2$。 一开始，所有格子都属于河流。城市们计划轮流选择一个格子将其填成陆地，依次进行，直到无法再有格子被填为陆地为止。 然而，这条河流同时也是重要的贸易航道。城市们必须确保船只仍然能从河流一端通航到另一端。更正式地说，如果某个格子 $(r,c)$ 已经被填为陆地，则不允许再将 $(r-1,3-c)$、$(r,3-c)$ 或 $(r+1,3-c)$ 这三个格子填为陆地。 这两座城市关系并不好，每个城市都希望成为最后一个填格子的城市（他们并不关心各自填了多少格子，只关心谁最后一次填了格子）。现在已经有 $n$ 个格子被填为陆地。你的任务是：判断在当前局面下，假设两边均以最优策略行动，轮到操作的一方是否能够确保成为最后一个填格子的城市。

第一行包含两个整数 $r$ 和 $n$（$1 \leq r \leq 100, 0 \leq n \leq r$）。接下来的 $n$ 行，每行包含两个整数 $r_i$ 和 $c_i$（$1 \leq r_i \leq r, 1 \leq c_i \leq 2$），表示已经被填为陆地的格子的行和列。所有这些格子均各不相同，且它们的填充不会违反上述限制条件。

如果当前轮到操作方能确保自己成为最后一次填格子的人，输出 "WIN"；否则输出 "LOSE"。

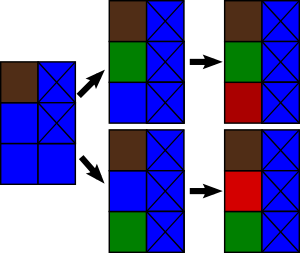
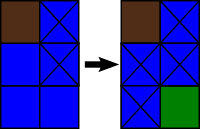
在第一个样例中，当前第一个城市有 3 个选择可以填的格子：$(2,1)$、$(3,1)$ 或 $(3,2)$。前两种选择会输，因为这样会让对方只剩下一个格子可以填。  而如果选择填 $(3,2)$，则不会留下可再填的格子，因此该城市获胜。  在第三个样例中，没有可被填为陆地的格子了。 由 ChatGPT 5 翻译