CF335C More Reclamation

In a far away land, there are two cities near a river. One day, the cities decide that they have too little space and would like to reclaim some of the river area into land. The river area can be represented by a grid with $ r $ rows and exactly two columns — each cell represents a rectangular area. The rows are numbered $ 1 $ through $ r $ from top to bottom, while the columns are numbered $ 1 $ and $ 2 $ . Initially, all of the cells are occupied by the river. The plan is to turn some of those cells into land one by one, with the cities alternately choosing a cell to reclaim, and continuing until no more cells can be reclaimed. However, the river is also used as a major trade route. The cities need to make sure that ships will still be able to sail from one end of the river to the other. More formally, if a cell $ (r,c) $ has been reclaimed, it is not allowed to reclaim any of the cells $ (r-1,3-c) $ , $ (r,3-c) $ , or $ (r+1,3-c) $ . The cities are not on friendly terms, and each city wants to be the last city to reclaim a cell (they don't care about how many cells they reclaim, just who reclaims a cell last). The cities have already reclaimed $ n $ cells. Your job is to determine which city will be the last to reclaim a cell, assuming both choose cells optimally from current moment.

The first line consists of two integers $ r $ and $ n $ ( $ 1

Output "WIN" if the city whose turn it is to choose a cell can guarantee that they will be the last to choose a cell. Otherwise print "LOSE".

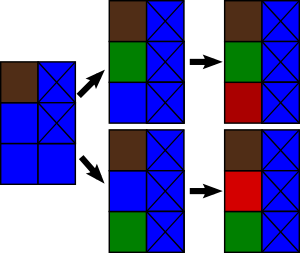In the first example, there are 3 possible cells for the first city to reclaim: $ (2,1) $ , $ (3,1) $ , or $ (3,2) $ . The first two possibilities both lose, as they leave exactly one cell for the other city. However, reclaiming the cell at $ (3,2) $ leaves no more cells that can be reclaimed, and therefore the first city wins. In the third example, there are no cells that can be reclaimed.