CF335E Counting Skyscrapers

一排摩天大楼被建造在一条直线上。摩天大楼的数量在 $2$ 到 $314!$ （314的阶乘，非常大的数字）之间等概率随机选取。每座摩天大楼的高度也被随机且独立选取，对于每个正整数 $i$，高度为 $i$ 的概率为 $2^{-i}$。一座高度为 $i$ 的摩天大楼，其楼层编号为 $0$ 到 $i-1$。 为了加快穿梭速度，在摩天大楼之间装设了若干条滑索。具体来说，如果某两座摩天大楼之间没有其他拥有第 $i$ 层的摩天大楼，则这两座摩天大楼的第 $i$ 层之间有一条滑索连接。 Alice 和 Bob 决定数一数摩天大楼的数量。 Alice 非常细致，她想要精确知道摩天大楼的数量。她从最左边的摩天大楼出发，计数器初始为 $1$，然后每移动到右边一座摩天大楼就计数加 $1$。她一直移动到最右边的摩天大楼。 Bob 很不耐烦，他想尽快完成。他从最左边的摩天大楼出发，计数器初始为 $1$。他会利用滑索直接从一座楼到另一座楼。每次，Bob 总是选择可用的、向右的最高楼层滑索，但由于恐高，他只会使用楼层编号不超过 $h$ 的滑索。当使用滑索时，Bob 移动得太快，无法计数他经过了多少座楼，因此他只会在计数器上加上 $2^i$，$i$ 是他当前所在的楼层编号。他一直重复直到到达最右边的摩天大楼。 来看如下例子。有 $6$ 栋楼，高度分别为 $1, 4, 3, 4, 1, 2$，$h=2$。Alice 从计数器 $1$ 开始，每次加 $1$，共加 $5$ 次，最终得到 $6$。Bob 从计数器 $1$ 开始，随后依次加上 $1$、$4$、$4$ 和 $2$，最终得到 $12$。注意，Bob 因为恐高，忽略了最高层的滑索（$h=2$）。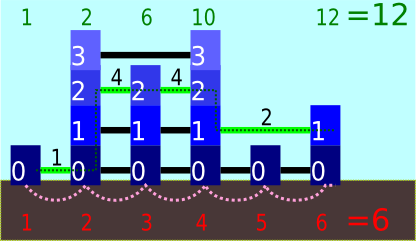  Bob 的计数器在图片上方，Alice 的在下方。所有滑索均已显示。Bob 的路径为绿色虚线，Alice 的为粉色虚线。摩天大楼的楼层已编号，Bob 使用过的滑索边标示了他计数器上的增量。 当 Alice 和 Bob 都到达最右边的摩天大楼后，他们会比较各自的计数器。你会得到 Alice 或 Bob 的计数器值，需要计算另一个人计数器的期望值。

输入的第一行是一个姓名，字符串 "Alice" 或 "Bob"。 第二行为两个整数 $n$ 和 $h$，$2 \leq n \leq 30000$，$0 \leq h \leq 30$。如果第一行为 "Alice"，则 $n$ 表示 Alice 到达最右边时的计数器值，否则 $n$ 表示 Bob 到达最右边时的计数器值；$h$ 表示 Bob 愿意使用的最高楼层编号。

输出一个实数，若给出的是 Bob 的计数器值，则输出 Alice 计数器的期望值；若给出的是 Alice 的计数器值，则输出 Bob 计数器的期望值。 你的答案如果绝对误差或相对误差不超过 $10^{-9}$ 即被视为正确。

在第一个样例中，Bob 的计数器以 $62.5\%$ 的概率为 $3$，$25\%$ 的概率为 $4$，$12.5\%$ 的概率为 $5$。 由 ChatGPT 5 翻译