CF336B Vasily the Bear and Fly

One beautiful day Vasily the bear painted $ 2m $ circles of the same radius $ R $ on a coordinate plane. Circles with numbers from $ 1 $ to $ m $ had centers at points $ (2R-R,0) $ , $ (4R-R,0) $ , $ ... $ , $ (2Rm-R,0) $ , respectively. Circles with numbers from $ m+1 $ to $ 2m $ had centers at points $ (2R-R,2R) $ , $ (4R-R,2R) $ , $ ... $ , $ (2Rm-R,2R) $ , respectively. Naturally, the bear painted the circles for a simple experiment with a fly. The experiment continued for $ m^{2} $ days. Each day of the experiment got its own unique number from $ 0 $ to $ m^{2}-1 $ , inclusive. On the day number $ i $ the following things happened: 1. The fly arrived at the coordinate plane at the center of the circle with number 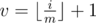 (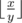 is the result of dividing number $ x $ by number $ y $ , rounded down to an integer). 2. The fly went along the coordinate plane to the center of the circle number 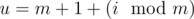 (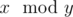 is the remainder after dividing number $ x $ by number $ y $ ). The bear noticed that the fly went from the center of circle $ v $ to the center of circle $ u $ along the shortest path with all points lying on the border or inside at least one of the $ 2m $ circles. After the fly reached the center of circle $ u $ , it flew away in an unknown direction. Help Vasily, count the average distance the fly went along the coordinate plane during each of these $ m^{2} $ days.

The first line contains two integers $ m,R $ ( $ 1

In a single line print a single real number — the answer to the problem. The answer will be considered correct if its absolute or relative error doesn't exceed $ 10^{-6} $ .

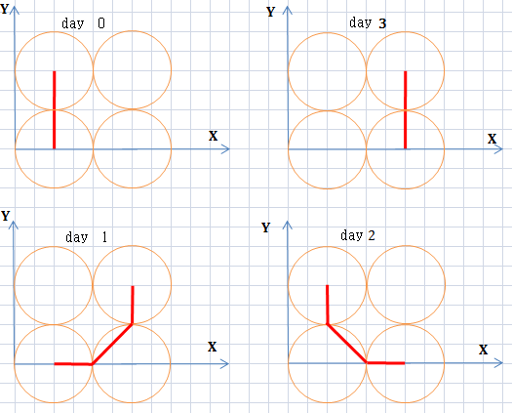
 Figure to the second sample