CF336B Vasily the Bear and Fly

一天，熊 Vasily 在坐标平面上画了 $2m$ 个半径为 $R$ 的圆。这些圆彼此半径相等，编号为 $1$ 到 $m$ 的圆的圆心分别坐标为 $(2R-R,0)$、$(4R-R,0)$、$\ldots$、$(2Rm-R,0)$。编号为 $m+1$ 到 $2m$ 的圆的圆心分别坐标为 $(2R-R,2R)$、$(4R-R,2R)$、$\ldots$、$(2Rm-R,2R)$。 熊画圆是为了做一个简单的苍蝇实验。这个实验持续了 $m^2$ 天，每一天都有一个唯一编号 $0$ 到 $m^2-1$。 在第 $i$ 天，发生以下事情： 1. 苍蝇来到编号为 $\left\lfloor \frac{i}{m} \right\rfloor+1$ 的圆心（$\left\lfloor \frac{x}{y} \right\rfloor$ 表示 $x$ 除以 $y$ 向下取整）。 2. 苍蝇飞向编号为 $(i \bmod m)+m+1$ 的圆心（$x \bmod y$ 表示 $x$ 除以 $y$ 的余数）。熊注意到苍蝇总是沿着最短的路径，从圆 $v$ 的圆心到圆 $u$ 的圆心，且路径始终位于至少一个圆的边界或内部。苍蝇到达圆 $u$ 的圆心后便飞走了。 请帮助 Vasily 计算，在 $m^2$ 天中，苍蝇每天实际走过的平均距离。

第一行包含两个整数 $m, R$（$1 \leq m \leq 10^5$，$1 \leq R \leq 10$）。

输出一个实数，即答案。如果你的答案与标准答案的绝对误差或相对误差不超过 $10^{-6}$，就会被认为是正确的。

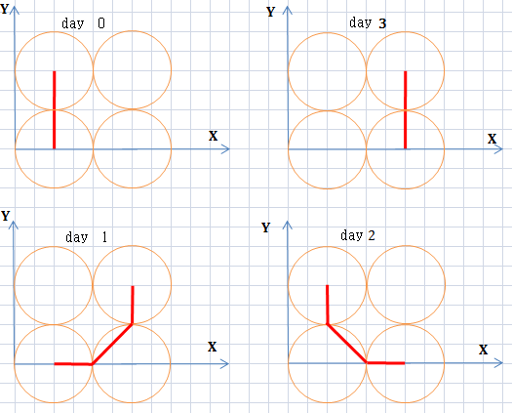
 图为第二个样例。 由 ChatGPT 5 翻译