CF336E Vasily the Bear and Painting Square

熊 Vasily 有两个最喜欢的整数 $n$ 和 $k$，以及一支铅笔。此外，他还有 $k$ 罐不同颜色的水彩颜料。所有颜料罐都以某种方式编号为 $1$ 到 $k$。第 $i$ 罐中装有第 $i$ 种颜色的颜料。 一开始，熊用铅笔在坐标平面上画了四条线段。所有线段都以点 $(0,0)$ 为一个端点。它们分别从点 $(0,2^n)$、$(0,-2^n)$、$(2^n,0)$、$(-2^n,0)$ 出发。然后，对于每个 $i=1,2,\ldots,n$，熊又画了两个正方形。第一个正方形的顶点坐标是：$(2^{i},0)$，$(-2^{i},0)$，$(0,-2^{i})$，$(0,2^{i})$。第二个正方形的顶点坐标是：$(-2^{i-1},-2^{i-1})$，$(-2^{i-1},2^{i-1})$，$(2^{i-1},-2^{i-1})$，$(2^{i-1},2^{i-1})$。之后，熊又画了一个正方形，其顶点分别为 $(1,0)$、$(-1,0)$、$(0,-1)$、$(0,1)$。上述所有点组成了点集 $A$。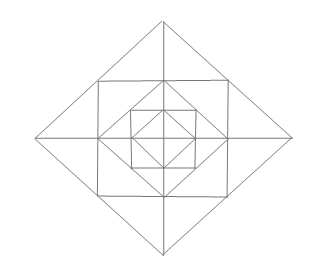  $n=0$ 时的最终图形示例  $n=2$ 时的最终图形示例 熊打算用 $k$ 步为图形着色。第 $i$ 步操作包括以下阶段： 1. 熊从点集 $A$ 中选择 3 个互不相同的点，使得这三点中任意两点之间都存在一条图上的线段。所选的点和线段围成的区域要求内不能包含已涂色的点。 2. 熊将由所选三点和线段围成的区域，用第 $i$ 种颜色涂色。 注意，在第 $k$ 步之后，图形的部分区域可能依然未被涂色。 熊现在请你计算，将他的图形涂色的方法有多少种。一次涂色方法是 $k$ 步操作中每步所选三个点集合的有序序列。如果存在某个 $i$（$1\leq i \leq k$），使得两种方法第 $i$ 步选的点集合不同，则认为这两种方法是不同的。由于答案可能很大，只需将答案对 $1000000007$（$10^9+7$）取模输出即可。

第一行包含用空格分隔的两个整数 $n$ 和 $k$（$0\leq n,k\leq 200$）。

输出一个整数，表示将图形着色的方法数，答案对 $1000000007$ 取模。

由 ChatGPT 5 翻译