CF337E Divisor Tree

一个“因子树”是满足以下条件的有根树： - 树的每个顶点都包含一个正整数。 - 树中所有叶子节点上的数字都是质数。 - 对于任意一个非叶子节点，其上写的数字等于其所有孩子节点上的数字之积。 Manao 有 $n$ 个互不相同的整数 $a_1, a_2, ..., a_n$。他尝试构建一个包含每个这些数字的因子树。也就是说，对于每个 $a_i$，树中至少有一个顶点包含 $a_i$。 Manao 喜欢简洁的风格，但他构建的树太大了。请帮助 Manao 求出满足条件的因子树中最少有多少个顶点。

第一行包含一个整数 $n$（$1 \leq n \leq 8$）。 第二行包含 $n$ 个互不相同的正整数 $a_i$（$2 \leq a_i \leq 10^{12}$）。

输出一个整数，表示至少需要多少个顶点的因子树，能够包含所有 $a_i$。

样例 1：最小的因子树如下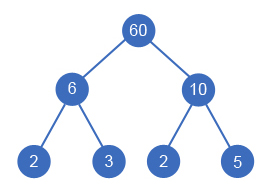： 样例 2：在这种情况下，可以构建如下的因子树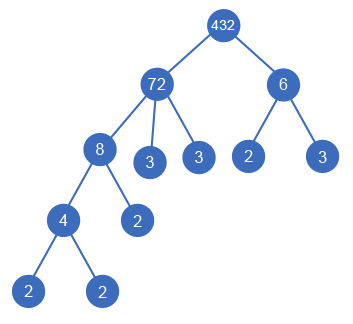： 样例 3：注意，因子树可以仅由一个顶点组成。 由 ChatGPT 5 翻译