CF342D Xenia and Dominoes

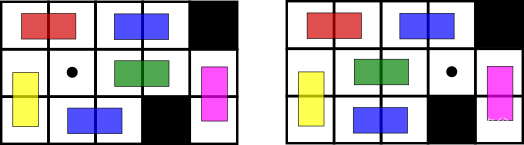
Xenia非常喜欢拼图。她特别喜欢由多米诺骨牌组成的拼图。图片中就是一个这样的拼图。  一个拼图是一个 $3\times n$ 的网格，除去一些禁止格（图中的黑色正方形）之外都包含多米诺骨牌。一个拼图被称作合法当它符合以下条件： - 每个多米诺骨牌覆盖正好两个非禁止格； - 没有两个多米诺骨牌覆盖桌子上的同一块区域； - 有且仅有一个非禁止格没被任何多米诺骨牌覆盖（图中的圆点）。 要完成一个拼图，你需要用若干步把空格子从开始位置移动某个指定位置。一步移动是在保证拼图合法的情况下，把一个多米诺骨牌移到空格子里。**横向的多米诺骨牌只能横向移动，纵向的多米诺骨牌只能纵向移动**。你不能旋转多米诺骨牌。上图表示了一个合法的移动。 Xenia 有一个 $3\times n$ 的有一些禁止格和一个标记格的网格。Xenia 还有很多完全一样的多米诺骨牌。现在 Xenia 想知道，如果她把多米诺骨牌放在桌子上，能有多少种不同的合法的拼图。同时，Xenia 要求圆圈标记的格子没有被覆盖。这个拼图还必须至少能移动一次。**所有与标记格有公共点的格子不是禁止格。** 请帮 Xenia 计算上述拼图的总数。这个数字可能很大，所以请输出它对 $10^9+7$ 取模的余数。

第一行一个整数 $n$，表示拼图的大小。接下来 $3$ 行，每行 $n$ 个字符，描述这个网格。第 $i$ 行的第 $j$ 个字符 - 若为 `X` 则表示对应的格子为禁止块； - 若为 `.` 表示非禁止块； - 若为 `O` 表示它是圆圈标记的。

一行一个数，问题的答案对 $10^9+7$ 取模的值。

对于所有数据，$3\leq n\leq 10^4$， 保证有且仅有一个标记格。所有与标记格有公共点的格子不是禁止格。