CF346E Doodle Jump

在 Doodle Jump 游戏中，玩家的目标是引导“四腿生物” The Doodler 蹦跳在一系列无尽的平台上，不能掉下来。——引自 Wikipedia。 这是一款非常受欢迎的游戏，xiaodao 很喜欢。有一天，xiaodao 在玩游戏时疑惑：会不会存在因为 The Doodler 的跳跃能力有限而无法到达的平台？请考虑如下问题。 有 $n$ 个平台。第 $x$ （$1\leq x \leq n$）个平台的高度为 $a\cdot x \bmod p$，其中 $a$ 和 $p$ 是互质的正整数。Doodler 最多能跳跃的高度为 $h$。也就是说，若 $h_2 - h_1 \leq h$ 并且 $h_1 < h_2$，那么 Doodler 能从高度 $h_1$ 跳到高度 $h_2$。一开始，Doodler 站在地面，地面的高度为 $0$。问题是，Doodler 能否到达最高的平台。 举例来说，当 $a=7$，$n=4$，$p=12$，$h=2$ 时，四个平台的高度分别为 $7$、$2$、$9$、$4$，如下面图片所示。第一次跳跃时 Doodler 能跳到高度为 $2$ 的平台，第二次跳跃能跳到高度为 $4$ 的平台，但之后无法再跳到任何更高的平台。因此，它无法到达最高的平台。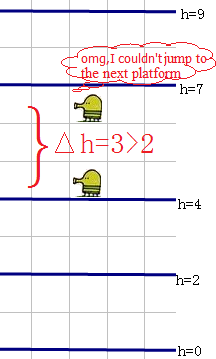  用户 xiaodao 思考了很久还是没有想出解法，于是请你帮忙。且她有许多组问题实例需要解答。你需要依次解答这些问题。

第一行包含一个整数 $t$（$1\leq t\leq 10^4$），表示问题实例的个数。之后 $t$ 行，每行包含四个整数 $a$、$n$、$p$ 和 $h$（$1\leq a\leq 10^9$，$1\leq n < p \leq 10^9$，$0\leq h \leq 10^9$）。保证 $a$ 和 $p$ 互质。

对于每个问题实例，如果 Doodler 能到达最高的平台，输出 "YES"；否则输出 "NO"。

由 ChatGPT 5 翻译