CF354D Transferring Pyramid

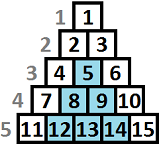
Vasya 和 Petya 使用一种有趣的数据存储结构：金字塔。 这个金字塔有 $n$ 行，第 $i$ 行包含 $i$ 个格子。每一行相对于上一行向左移动了半个格子的宽度。格子的编号为 $1$ 到 $\frac{n(n+1)}{2}$，如下图所示。 当 $n=5$ 时，金字塔的示例如下：  该数据结构可以执行两种类型的操作： 1. 修改指定格子的值。操作格式为三个整数：$"t\ i\ v"$，其中 $t=1$（操作类型），$i$ 表示要修改的格子的编号，$v$ 表示赋给该格子的值。 2. 修改某个子金字塔的所有格子的值。下图中突出显示了顶点为格子 $5$ 的子金字塔。操作格式为 $s+2$ 个整数：$"t\ i\ v_{1}\ v_{2}\ ...\ v_{s}"$，其中 $t=2$，$i$ 表示子金字塔顶点格子的编号，$s$ 表示子金字塔包含的格子数，$v_j$ 表示第 $j$ 个格子要赋的值。 更正式地说：顶点在第 $k$ 行第 $i$ 个格子的子金字塔（例如第 $5$ 个格子是第三行第二个格子）包含从第 $k$ 行到第 $n$ 行对应的格子。第 $k+p$ 行包含从第 $i$ 个到第 $i+p$ 个格子（$0\leq p\leq n-k$）。 Vasya 和 Petya 各自有一个完全相同的金字塔。Vasya 对自己的金字塔进行了一些格子的修改，现在他希望把自己的这些更改发送给 Petya。为此，他需要找到一系列操作，使得 Petya 执行后效果与自己一致。在所有可能的操作序列中，Vasya 要选择包含数字数量最少的那一个。 给定一个有 $n$ 行的金字塔和 $k$ 个已被修改的格子，请找出一种操作序列，使得每一个被修改的格子都至少被某个操作修改覆盖。要求在所有可能的方案中，选择总数字数量最少的那一个。

第一行包含两个整数 $n$ 和 $k$（$1\leq n,k\leq10^5$）。 接下来 $k$ 行，每行包含两个整数 $r_i$ 和 $c_i$（$1\leq c_i\leq r_i\leq n$），表示被修改的格子的行号和该行中的编号。所有格子互不相同。

输出一个整数，表示最终操作序列所包含的数字总数。

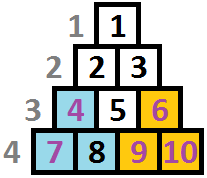
第一组样例的一种可能解由两次操作组成： $2\ 4\ v_{4}\ v_{7}\ v_{8}$ $2\ 6\ v_{6}\ v_{9}\ v_{10}$ 图中被修改的格子已经用彩色高亮表示。第一种操作用蓝色高亮子金字塔，第二种操作用黄色高亮子金字塔：  由 ChatGPT 5 翻译