CF356D Bags and Coins
题目描述
小时候你一定听说过关于袋子和硬币的谜题。无论如何,这里有一个版本:
一匹马有三个袋子。第一个袋子有一个硬币,第二个袋子有一个硬币,第三个袋子有三个硬币。总共,这匹马在袋子里有三个硬币。这怎么可能呢?
答案很简单。第三个袋子里实际上有一个硬币和另外两个袋子。
本题是这个童年谜题的推广。你有 $n$ 个袋子。你知道第 $1$ 个袋子里有 $a_{1}$ 个硬币,第 $2$ 个袋子有 $a_{2}$ 个硬币,……第 $n$ 个袋子有 $a_{n}$ 个硬币。总共一共有 $s$ 个硬币。请找出一种方式安排袋子和硬币,使得它们满足上述描述,否则输出不可能。
输入格式
第一行包含两个整数 $n$ 和 $s$($1 \leq n, s \leq 70000$)——袋子的数量和硬币总数。第二行包含 $n$ 个整数 $a_{1}, a_{2}, ..., a_{n}$($1 \leq a_{i} \leq 70000$),其中 $a_{i}$ 表示第 $i$ 个袋子里有多少硬币。
输出格式
如果不存在符合条件的安排,输出 $-1$。
否则,输出 $n$ 行,第 $i$ 行描述第 $i$ 个袋子的内容。该行的第一个数字 $c_{i}$($0 \leq c_{i} \leq a_{i}$)代表直接放在第 $i$ 个袋子里的硬币数量(不包括其内部袋子里的硬币)。第二个数字 $k_{i}$($0 \leq k_{i} < n$)表示直接放在第 $i$ 个袋子里的袋子的数量(不包括这些袋子内部嵌套的其它袋子)。接下来是 $k_{i}$ 个整数,表示直接放在第 $i$ 个袋子里的袋子的编号。
最终方案中总体硬币数必须恰好为 $s$。对于每个袋子 $i$,最终统计该袋子内(包括其内部所有嵌套袋子)硬币总数,应等于 $a_{i}$。
没有任何一个袋子可以被直接放进超过一个袋子里。袋子之间可以多层嵌套(详见第二个样例)。如果存在多种合理的方案,你可以输出任何一种。
说明/提示
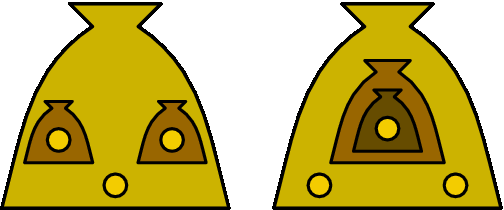
下方图片展示了样例中的两种可行方案。左图对应第一个样例,右图对应第二个样例。
由 ChatGPT 5 翻译