CF359A Table

Simon 有一个由 $n$ 行 $m$ 列组成的矩形表格。Simon 将表格的行自上而下编号，从 $1$ 开始，列自左到右编号，也是从 $1$ 开始。我们用一对数字 $(x, y)$ 表示第 $x$ 行第 $y$ 列的格子。表格的四个角分别为：$(1,1)$、$(n,1)$、$(1,m)$、$(n,m)$。 Simon 认为表中某些格子是“好”的。另外，已知没有任何一个“好”格子在表格的四个角上。 最初所有格子都是无色的。Simon 想要将表格中的所有格子都染色。每次操作时，他可以选择任意一个“好”格子 $(x_{1}, y_{1})$，再任选表格的一个角 $(x_{2}, y_{2})$，然后将满足 $min(x_{1}, x_{2}) \leq p \leq max(x_{1}, x_{2})$，$min(y_{1}, y_{2}) \leq q \leq max(y_{1}, y_{2})$ 的所有格子 $(p,q)$ 染色。 请你帮助 Simon，求出将所有格子染色所需的最少操作次数。注意，你可以多次重复染色同一个格子。

第一行包含两个正整数 $n, m$，表示表格的行数和列数，满足 $3 \leq n, m \leq 50$。 接下来的 $n$ 行，每行包含 $m$ 个用空格分隔的整数 $a_{i1},a_{i2},...,a_{im}$。如果 $a_{ij}=0$，表示格子 $(i,j)$ 不是“好”格子；如果 $a_{ij}=1$，表示$(i,j)$ 是“好”格子。保证至少存在一个“好”格子，并保证四个角都不是“好”格子。

输出一个整数，表示将所有格子染色所需的最少操作次数。

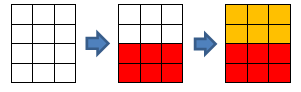
在第一个样例中，操作顺序可以如下：  - 第一次选择格子 $(2,2)$ 和角 $(1,1)$。 - 第二次选择格子 $(2,2)$ 和角 $(3,3)$。 - 第三次选择格子 $(2,2)$ 和角 $(3,1)$。 - 第四次选择格子 $(2,2)$ 和角 $(1,3)$。 在第二个样例中，操作顺序可以如下：  - 第一次选择格子 $(3,1)$ 和角 $(4,3)$。 - 第二次选择格子 $(2,3)$ 和角 $(1,1)$。 由 ChatGPT 5 翻译