CF359C Prime Number

Simon 有一个质数 $x$ 和一个非负整数数组 $a_1,a_2,...,a_n$。 Simon 非常喜欢分数。今天他在纸上写下了如下的数字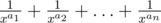：。在把所有分数通分并相加之后，他得到了一个分数：，其中 $t=x^{a_{1}+a_{2}+...+a_{n}}$。现在 Simon 想要将得到的分数约分。 请帮助他，找到 $s$ 和 $t$ 的最大公约数。由于最大公约数可能非常大，请输出答案对 $1000000007$（$10^9+7$）取模后的结果。

第一行包含两个正整数 $n$ 和 $x$（$1 \leq n \leq 10^5$，$2 \leq x \leq 10^9$）——数组的长度和那个质数。 第二行包含 $n$ 个用空格分隔的整数 $a_1,a_2,...,a_n$（$0 \leq a_1 \leq a_2 \leq ... \leq a_n \leq 10^9$）。

输出一个整数，表示问题的答案，对 $1000000007$（$10^9+7$）取模后的结果。

在第一个样例中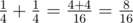，。因此，答案为 $8$。 在第二个样例中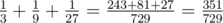，。答案为 $27$，因为 $351=13 \cdot 27$，$729=27 \cdot 27$。 在第三个样例中，答案为 $1073741824 \bmod 1000000007 = 73741817$。 在第四个样例中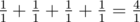，。因此答案为 $1$。 由 ChatGPT 5 翻译