CF360B Levko and Array
题目描述
Levko 有一个由整数构成的数组 $a_{1}, a_{2}, \ldots, a_{n}$。但他一点也不喜欢这个数组。
Levko 认为数组 $a$ 的美丽程度直接取决于值 $c(a)$,其计算公式如下:
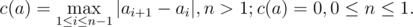
$ c(a) $ 越小,数组越美丽。现在,Levko 想要改变自己的数组,让它变得更美观。具体来说,Levko 最多可以更改 $k$ 个数组元素(可以将其替换为任意整数)。当然,他应当尽可能让数组变得更美丽。
请帮助 Levko 计算,他能够得到的最小 $c(a)$ 值是多少。
输入格式
第一行包含两个整数 $n$ 和 $k$($1 \leq k \leq n \leq 2000$)。
第二行包含 $n$ 个用空格分隔的整数 $a_{1}, a_{2}, \ldots, a_{n}$($-10^{9} \leq a_{i} \leq 10^{9}$)。
输出格式
输出一个整数——Levko 能获得的最小 $c(a)$ 值。
说明/提示
在第一个样例中,Levko 可以修改第 2 个和第 4 个元素,使得数组变为:$4, 4, 4, 4, 4$。
在第三个样例中,他可以得到数组:$1, 2, 3, 4, 5, 6$。
由 ChatGPT 5 翻译