CF363E Two Circles

Let's assume that we are given an $ n×m $ table filled by integers. We'll mark a cell in the $ i $ -th row and $ j $ -th column as $ (i,j) $ . Thus, $ (1,1) $ is the upper left cell of the table and $ (n,m) $ is the lower right cell. We'll assume that a circle of radius $ r $ with the center in cell $ (i_{0},j_{0}) $ is a set of such cells $ (i,j) $ that 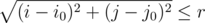. We'll consider only the circles that do not go beyond the limits of the table, that is, for which $ r+1

The first line contains three integers $ n $ , $ m $ and $ r $ ( $ 2

Print two integers — the maximum sum of numbers in the cells that are located into two non-intersecting circles and the number of pairs of non-intersecting circles with the maximum sum. If there isn't a single pair of non-intersecting circles, print 0 0.