CF370A Rook, Bishop and King

Little Petya is learning to play chess. He has already learned how to move a king, a rook and a bishop. Let us remind you the rules of moving chess pieces. A chessboard is 64 square fields organized into an $ 8×8 $ table. A field is represented by a pair of integers $ (r,c) $ — the number of the row and the number of the column (in a classical game the columns are traditionally indexed by letters). Each chess piece takes up exactly one field. To make a move is to move a chess piece, the pieces move by the following rules: - A rook moves any number of fields horizontally or vertically. - A bishop moves any number of fields diagonally. - A king moves one field in any direction — horizontally, vertically or diagonally. 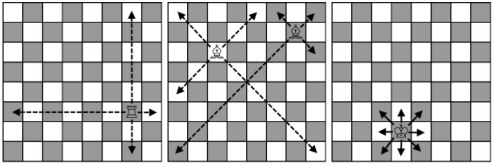The pieces move like thatPetya is thinking about the following problem: what minimum number of moves is needed for each of these pieces to move from field $ (r_{1},c_{1}) $ to field $ (r_{2},c_{2}) $ ? At that, we assume that there are no more pieces besides this one on the board. Help him solve this problem.

The input contains four integers $ r_{1},c_{1},r_{2},c_{2} $ ( $ 1

Print three space-separated integers: the minimum number of moves the rook, the bishop and the king (in this order) is needed to move from field $ (r_{1},c_{1}) $ to field $ (r_{2},c_{2}) $ . If a piece cannot make such a move, print a 0 instead of the corresponding number.