CF371A K-Periodic Array

This task will exclusively concentrate only on the arrays where all elements equal 1 and/or 2. Array $ a $ is $ k $ -period if its length is divisible by $ k $ and there is such array $ b $ of length $ k $ , that $ a $ is represented by array $ b $ written exactly 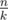 times consecutively. In other words, array $ a $ is $ k $ -periodic, if it has period of length $ k $ . For example, any array is $ n $ -periodic, where $ n $ is the array length. Array $ [2,1,2,1,2,1] $ is at the same time 2-periodic and 6-periodic and array $ [1,2,1,1,2,1,1,2,1] $ is at the same time 3-periodic and 9-periodic. For the given array $ a $ , consisting only of numbers one and two, find the minimum number of elements to change to make the array $ k $ -periodic. If the array already is $ k $ -periodic, then the required value equals $ 0 $ .

The first line of the input contains a pair of integers $ n $ , $ k $ ( $ 1

Print the minimum number of array elements we need to change to make the array $ k $ -periodic. If the array already is $ k $ -periodic, then print 0.

In the first sample it is enough to change the fourth element from 2 to 1, then the array changes to $ [2,1,2,1,2,1] $ . In the second sample, the given array already is 4-periodic. In the third sample it is enough to replace each occurrence of number two by number one. In this case the array will look as $ [1,1,1,1,1,1,1,1,1] $ — this array is simultaneously 1-, 3- and 9-periodic.