Circling Round Treasures

给你一个 $N \times M$ 的地图（$N,M \le 20$），地图上 `#` 表示障碍物，`B` 表示炸弹，数字表示宝藏序号（宝藏+炸弹个数 $\le 8$），每个宝藏有价值（$-200 \le v \le 200$），`S` 表示出发点。每次移动可以从一个格子移动到相邻格子（上下左右）。寻找一条路径从 `S` 出发再回到 `S` 的封闭路径，移动步数记为 $K$，这个路径所包围的宝藏价值总和记为 $V$，则这条路径的价值为 $V - K$。题目即是求可行的最大的路径价值，并且不能包围炸弹。 ## 输入格式： 第一行两个整数 $N, M$ 表示地图的长和宽 接下来 $N$ 行，每行 $M$ 个字符，描述整个地图，地图只可能包含如下字符: 字符 `B` 表示炸弹； 字符 `S` 表示起点,保证有且只有一个； 数字 $c$（$1 \sim 8$）代表宝藏标号，宝藏和炸弹加起来最多只有 $8$ 个； 字符 `.` 表示空白格； 字符 `#` 表示障碍物(墙)； 假设地图包含 $t$ 个宝藏，接下来 $t$ 行，每行一个整数 $v_i$（$-200 \le v_i \le 200$），依序表示第 $i$ 个宝藏的价值。 ## 输出格式： 一个整数，即能够获得的最大价值 感谢@xjdx 提供的翻译

You have a map as a rectangle table. Each cell of the table is either an obstacle, or a treasure with a certain price, or a bomb, or an empty cell. Your initial position is also given to you. You can go from one cell of the map to a side-adjacent one. At that, you are not allowed to go beyond the borders of the map, enter the cells with treasures, obstacles and bombs. To pick the treasures, you need to build a closed path (starting and ending in the starting cell). The closed path mustn't contain any cells with bombs inside. Let's assume that the sum of the treasures' values that are located inside the closed path equals $ v $ , and besides, you've made $ k $ single moves (from one cell to another) while you were going through the path, then such path brings you the profit of $ v-k $ rubles. Your task is to build a closed path that doesn't contain any bombs and brings maximum profit. Note that the path can have self-intersections. In order to determine if a cell lies inside a path or not, use the following algorithm: 1. Assume that the table cells are points on the plane (the table cell on the intersection of the $ i $ -th column and the $ j $ -th row is point $ (i,j) $ ). And the given path is a closed polyline that goes through these points. 2. You need to find out if the point $ p $ of the table that is not crossed by the polyline lies inside the polyline. 3. Let's draw a ray that starts from point $ p $ and does not intersect other points of the table (such ray must exist). 4. Let's count the number of segments of the polyline that intersect the painted ray. If this number is odd, we assume that point $ p $ (and consequently, the table cell) lie inside the polyline (path). Otherwise, we assume that it lies outside.

The first line contains two integers $ n $ and $ m $ $ (1<=n,m<=20) $ — the sizes of the table. Next $ n $ lines each contains $ m $ characters — the description of the table. The description means the following: - character "B" is a cell with a bomb; - character "S" is the starting cell, you can assume that it's empty; - digit $ c $ (1-8) is treasure with index $ c $ ; - character "." is an empty cell; - character "\#" is an obstacle. Assume that the map has $ t $ treasures. Next $ t $ lines contain the prices of the treasures. The $ i $ -th line contains the price of the treasure with index $ i $ , $ v_{i} $ $ (-200<=v_{i}<=200) $ . It is guaranteed that the treasures are numbered from 1 to $ t $ . It is guaranteed that the map has not more than 8 objects in total. Objects are bombs and treasures. It is guaranteed that the map has exactly one character "S".

Print a single integer — the maximum possible profit you can get.

4 4
....
.S1.
....
....
10

2

7 7
.......
.1###2.
.#...#.
.#.B.#.
.3...4.
..##...
......S
100
100
100
100

364

7 8
........
........
....1B..
.S......
....2...
3.......
........
100
-100
100

0

1 1
S

0

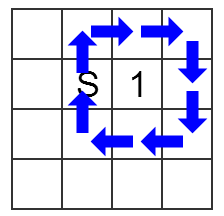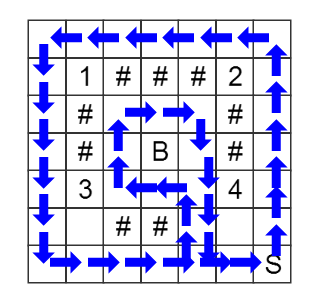In the first example the answer will look as follows. In the second example the answer will look as follows. In the third example you cannot get profit. In the fourth example you cannot get profit as you cannot construct a closed path with more than one cell.