CF380B Sereja and Tree
Description
Sereja adores trees. Today he came up with a revolutionary new type of binary root trees.
His new tree consists of $ n $ levels, each vertex is indexed by two integers: the number of the level and the number of the vertex on the current level. The tree root is at level $ 1 $ , its index is $ (1,1) $ . Here is a pseudo code of tree construction.
`
//the global data are integer arrays cnt[], left[][], right[][]
cnt[1] = 1;
fill arrays left[][], right[][] with values -1;
for(level = 1; level < n; level = level + 1){
cnt[level + 1] = 0;
for(position = 1; position
//the global data are integer arrays cnt[], left[][], right[][]
cnt[1] = 1;
fill arrays left[][], right[][] with values -1;
for(level = 1; level < n; level = level + 1){
cnt[level + 1] = 0;
for(position = 1; position
Input Format
The first line contains integers $ n $ and $ m $ $ (1
Output Format
For each operation of the second type, print the answer on a single line.
Explanation/Hint
You can find the definitions that are used while working with root trees by this link: http://en.wikipedia.org/wiki/Tree\_(graph\_theory)
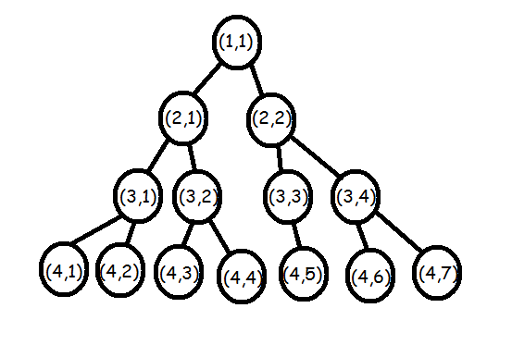
You can see an example of a constructed tree at $ n=4 $ below.