CF380D Sereja and Cinema

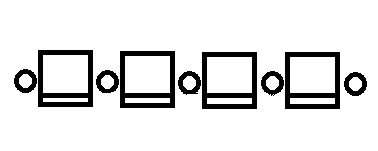
Sereja 的电影院有 $n$ 个座位在一个大屏幕前排成一行，在每个座位的左边和右边都有放置个人物品的凹槽，任何两个相邻的座位恰好有一个共享的凹槽，下图显示了 $n=4$ 的座位和凹槽的分布。  今天是一部名为《 Dry Hard 》的电影的首映式，所有票都卖完了。所有人会排队一个一个地进入影厅。当一个人进入影厅，他立即占据他的座位和他旁边的所有空的凹槽。如果没有空的凹槽，他会非常沮丧，然后离开。 人们不是固定不变的，所以很难预测观众进入大厅的顺序。Sereja 知道坐在某些位置的观众排在队列的位置。其他人可能排在其余任何位置。 作为一个程序员和数学家，Sereja 想知道：有多少种方式可以使得没有人沮丧而离开。因为答案很大，输出模 $1000000007$。

第一行包含一个整数 $n$。（$1\leq n\leq 10^5$） 第二行包含 $n$ 个非负整数，第 $i$ 个数表示坐在第 $i$ 个位置的观众排在队列中的位置，保证该数不超过 $n$，且不存在两个非零数相同。若第 $i$ 个数为 $0$，表示坐在第 $i$ 个位置的观众排在队列中的位置不确定。

一行一个整数，表示答案除以 $1000000007$ 后的余数。