CF385C Bear and Prime Numbers

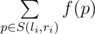最近，小熊开始学习数据结构，遇到了如下问题。 给定一个长度为 $n$ 的整数序列 $x_1, x_2, ..., x_n$，以及 $m$ 个查询，每个查询由两个整数 $l_i, r_i$ 描述。令 $f(p)$ 表示满足 $x_k$ 能被 $p$ 整除的下标 $k$ 的个数。对于每个查询 $l_i, r_i$，需要计算如下和： ，其中 $S(l_i, r_i)$ 表示区间 $[l_i, r_i]$（包含区间两端）中的所有质数构成的集合。 请帮助小熊解决这个问题。

第一行包含一个整数 $n$，满足 $1 \le n \le 10^6$。 第二行包含 $n$ 个整数 $x_1, x_2, ..., x_n$，满足 $2 \le x_i \le 10^7$。这些数不一定互不相同。 第三行包含一个整数 $m$，满足 $1 \le m \le 50000$。接下来的 $m$ 行中，每行包含一对用空格分隔的整数 $l_i$ 和 $r_i$，满足 $2 \le l_i \le r_i \le 2 \cdot 10^9$，表示一个查询。

输出 $m$ 个整数，依次为每个查询的答案。

以第一个样例为例。总体上，该样例有 3 个查询。 1. 第一个查询 $l=2$，$r=11$，需要计算 $f(2)+f(3)+f(5)+f(7)+f(11)=2+1+4+2+0=9$。 2. 第二个查询 $l=3$，$r=12$，需要计算 $f(3)+f(5)+f(7)+f(11)=1+4+2+0=7$。 3. 第三个查询 $l=4$，$r=4$，由于该区间没有质数，因此答案为 $0$。 由 ChatGPT 5 翻译