CF385C Bear and Prime Numbers

Recently, the bear started studying data structures and faced the following problem. You are given a sequence of integers $ x_{1},x_{2},...,x_{n} $ of length $ n $ and $ m $ queries, each of them is characterized by two integers $ l_{i},r_{i} $ . Let's introduce $ f(p) $ to represent the number of such indexes $ k $ , that $ x_{k} $ is divisible by $ p $ . The answer to the query $ l_{i},r_{i} $ is the sum: 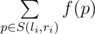, where $ S(l_{i},r_{i}) $ is a set of prime numbers from segment $ [l_{i},r_{i}] $ (both borders are included in the segment). Help the bear cope with the problem.

The first line contains integer $ n $ $ (1

Print $ m $ integers — the answers to the queries on the order the queries appear in the input.

Consider the first sample. Overall, the first sample has 3 queries. 1. The first query $ l=2 $ , $ r=11 $ comes. You need to count $ f(2)+f(3)+f(5)+f(7)+f(11)=2+1+4+2+0=9 $ . 2. The second query comes $ l=3 $ , $ r=12 $ . You need to count $ f(3)+f(5)+f(7)+f(11)=1+4+2+0=7 $ . 3. The third query comes $ l=4 $ , $ r=4 $ . As this interval has no prime numbers, then the sum equals 0.