CF394E Lightbulb for Minister

教育部长要来了！自然，没有人想在这位尊贵的客人面前表现不佳。然而，在到达前两个小时，我们发现其中一个班级的灯泡坏了——出于某种原因，它没有获得足够的能量。很快就找到了解决方案：我们只需要改变灯泡的位置，使其获得最大能量。 大家都知道，灯泡的功率等于 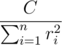，其中 $ C $ 是某个常数，$ r_{i} $ 是灯泡到第 $ i $ 个发电机的欧几里得距离。因此，我们的任务是最小化 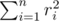。当然，我们知道所有发电机的位置。 灯泡应该位于教室的天花板上。教室的天花板是一个严格凸起的 $ m $ 边形（教室本身是一个底面为严格凸起的 $ m $ 边形的直棱柱）。请帮助找到灯泡的最佳位置。假设所有发电机都在教室天花板的平面上。考虑教室天花板所在的平面已经引入了笛卡尔坐标系。

第一行包含整数 $ n $ $ (2 \le n \le 10^{5}) $ — 表示发电机的数量。接下来的 $ n $ 行，每行包含一对整数 $ x_{i} $ , $ y_{i} $ ，表示第 $ i $ 个发电机在教室天花板平面上的坐标。保证没有两个发电机位于同一位置。 下一行包含整数 $ m $ $ (3 \le m \le 10^{5}) $ — 表示描述教室天花板的凸多边形中的顶点数量。接下来的 $ m $ 行，每行包含一对整数 $ p_{i},q_{i} $ ，表示多边形按顺时针顺序的第 $ i $ 个点的坐标。保证多边形是严格凸起的。 所有坐标的绝对值均不超过 $ 10^{6} $ 。

打印一个实数——即从发电机到灯泡最优位置的距离的平方和的最小值。如果答案的绝对误差或相对误差不超过 $ 10^{-4} $，则认为该答案是有效的。

我们将严格凸多边形定义为具有以下性质的凸多边形：多边形的任意三个顶点不共线。