CF396A On Number of Decompositions into Multipliers

You are given an integer $ m $ as a product of integers $ a_{1},a_{2},...\ a_{n} $ 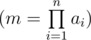. Your task is to find the number of distinct decompositions of number $ m $ into the product of $ n $ ordered positive integers. Decomposition into $ n $ products, given in the input, must also be considered in the answer. As the answer can be very large, print it modulo $ 1000000007 $ $ (10^{9}+7) $ .

The first line contains positive integer $ n $ ( $ 1

In a single line print a single number $ k $ — the number of distinct decompositions of number $ m $ into $ n $ ordered multipliers modulo $ 1000000007 $ $ (10^{9}+7) $ .

In the second sample, the get a decomposition of number 2, you need any one number out of three to equal 2, and the rest to equal 1. In the third sample, the possible ways of decomposing into ordered multipliers are \[7,5\], \[5,7\], \[1,35\], \[35,1\]. A decomposition of positive integer $ m $ into $ n $ ordered multipliers is a cortege of positive integers $ b={b_{1},b_{2},...\ b_{n}} $ such that 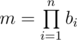. Two decompositions $ b $ and $ c $ are considered different, if there exists index $ i $ such that $ b_{i}≠c_{i} $ .