CF396D On Sum of Number of Inversions in Permutations

You are given a permutation $ p $ . Calculate the total number of inversions in all permutations that lexicographically do not exceed the given one. As this number can be very large, print it modulo $ 1000000007 $ $ (10^{9}+7) $ .

The first line contains a single integer $ n $ ( $ 1

Print a single number — the answer to the problem modulo $ 1000000007 $ $ (10^{9}+7) $ .

Permutation $ p $ of length $ n $ is the sequence that consists of $ n $ distinct integers, each of them is from $ 1 $ to $ n $ . An inversion of permutation $ p_{1},p_{2},...,p_{n} $ is a pair of indexes $ (i,j) $ , such that $ i<j $ and $ p_{i}>p_{j} $ . Permutation $ a $ do not exceed permutation $ b $ lexicographically, if either $ a=b $ or there exists such number $ i $ , for which the following logical condition fulfills: 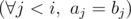 AND $ (a_{i}<b_{i}) $ .