CF398C Tree and Array

User ainta likes trees. This time he is going to make an undirected tree with $ n $ vertices numbered by integers from $ 1 $ to $ n $ . The tree is weighted, so each edge of the tree will have some integer weight. Also he has an array $ t $ : $ t[1],t[2],...,t[n] $ . At first all the elements of the array are initialized to $ 0 $ . Then for each edge connecting vertices $ u $ and $ v $ ( $ u<v $ ) of the tree with weight $ c $ , ainta adds value $ c $ to the elements $ t[u],t[u+1],...,t[v-1],t[v] $ of array $ t $ . Let's assume that $ d(u,v) $ is the total weight of edges on the shortest path between vertex $ u $ and vertex $ v $ . User ainta calls a pair of integers $ x,y $ ( $ 1

The first line contains a single integer $ n $ ( $ 5

Print $ n-1 $ lines containing the description of the edges. The $ i $ -th line should contain three space-separated integers $ u_{i},v_{i},c_{i} $ ( $ 1

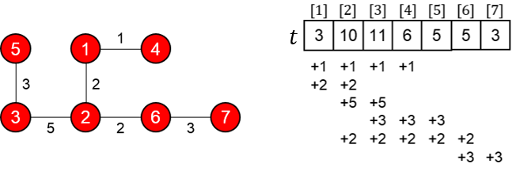
$ ⌊x⌋ $ is the largest integer not greater than $ x $ . You can find the definition of a tree by the following link: http://en.wikipedia.org/wiki/Tree\_(graph\_theory) You can also find the definition of the shortest path by the following link: http://en.wikipedia.org/wiki/Shortest\_path\_problem The tree and the array $ t $ in the sample output look like this: