CF398C Tree and Array

用户 ainta 喜欢树。这一次他打算构造一棵有 $n$ 个结点的无向树，结点编号为 $1$ 到 $n$。这颗树带有权值，也就是说每条边都有一个整数权重。 他还有一个数组 $t$：$t[1],t[2],...,t[n]$。一开始，数组的所有元素都被初始化为 $0$。然后，对于树上每条连接 $u$ 和 $v$ 的边（$u < v$）且权重为 $c$，用户 ainta 会把 $c$ 加到数组 $t$ 的 $t[u], t[u+1], ..., t[v-1], t[v]$ 这几个位置上。 记 $d(u,v)$ 为结点 $u$ 到结点 $v$ 间的最短路径经过的所有边的权值和。用户 ainta 称一对整数 $x, y$（$1 \leq x < y \leq n$）为“好对”当且仅当 $d(x, y) = t[x] + t[x+1] + ... + t[y-1] + t[y]$ 成立。 用户 ainta 希望能构造出至少 $\left\lfloor \frac{n^2}{4} \right\rfloor$ 对“好对”，但他没能构造出合适的树。请你帮 ainta 找到这样一棵树。

第一行包含一个整数 $n$（$5 \leq n \leq 10^5$）。

输出 $n-1$ 行，每行描述一条边。第 $i$ 行包含三个用空格分隔的整数 $u_{i}, v_{i}, c_{i}$（$1 \leq u_{i} < v_{i} \leq n; 1 \leq c_{i} \leq 10^5$），表示连接的两个结点和边的权重。 接下来输出 $\left\lfloor \frac{n^2}{4} \right\rfloor$ 行，每行包含两个用空格隔开的整数 $x_k$ 和 $y_k$（$1 \leq x_k < y_k \leq n$）。显然，$x_k, y_k$ 必须是一对好对。所有的配对都要互不相同——也就是说，对于所有 $j, k$，如果 $j \neq k$，必须满足 $x_j \neq x_k$ 或 $y_j \neq y_k$。 如果有多个合法方案，可以输出任意一个。

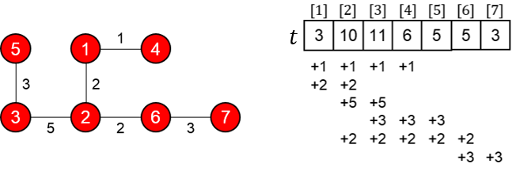
$\left\lfloor x \right\rfloor$ 表示不大于 $x$ 的最大整数。 你可以通过以下链接了解树的定义：http://en.wikipedia.org/wiki/Tree\_(graph\_theory) 你也可以通过以下链接了解最短路径的定义：http://en.wikipedia.org/wiki/Shortest\_path\_problem sample output 中展示的树和数组 $t$ 如下：  由 ChatGPT 5 翻译