CF402C Searching for Graph
题目描述
我们称一个有 $n$ 个顶点的无向图为 $p$-有趣图,如果满足以下条件:
- 该图恰好有 $2n+p$ 条边;
- 该图没有自环和重边;
- 对于任意整数 $k$ 且 $1 \leq k \leq n$,任意包含 $k$ 个顶点的子图最多包含 $2k+p$ 条边。
一个图的子图指的是该图某些顶点和这些顶点之间的某些边组成的图,要求这些边的两个端点都属于已选顶点集合。
你的任务是,构造一个包含 $n$ 个顶点的 $p$-有趣图。
输入格式
第一行包含一个整数 $t$($1 \leq t \leq 5$),表示测试数据的组数。接下来的 $t$ 行,每行包含两个用空格分隔的整数 $n$ 和 $p$($5 \leq n \leq 24$;$p \geq 0$;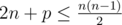),分别表示图的顶点数和兴趣值。
保证一定存在满足条件的图。
输出格式
对于每组测试数据,输出 $2n+p$ 行,每行两个用空格分隔的整数 $a_i, b_i$($1 \leq a_i, b_i \leq n$,且 $a_i \ne b_i$),表示一条边连接顶点 $a_i$ 和 $b_i$。顶点编号为 $1$ 到 $n$。
按输入顺序输出每组测试的答案。如果有多组解,输出任意一种都可以。
说明/提示
由 ChatGPT 5 翻译