CF402E Strictly Positive Matrix
题目描述
给定一个 $n \times n$ 的矩阵 $a$。我们将矩阵的行从上到下编号为 $1$ 到 $n$,列从左到右编号为 $1$ 到 $n$。用 $a_{ij}$ 表示第 $i$ 行第 $j$ 列的元素。
矩阵 $a$ 满足以下两个条件:
- 对于任意的 $i, j$ ($1 \leq i, j \leq n$),都有 $a_{ij} \geq 0$;
- 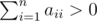。
如果对于任意的 $i, j$($1 \leq i, j \leq n$)都有 $b_{ij} > 0$,我们称矩阵 $b$ 是严格正的。你的任务是判断是否存在某个整数 $k \geq 1$,使得矩阵 $a^k$ 是严格正的。
输入格式
第一行包含一个整数 $n$($2 \leq n \leq 2000$),表示矩阵 $a$ 的行和列数。
接下来的 $n$ 行描述矩阵 $a$ 的每一行。第 $i$ 行包含 $n$ 个非负整数 $a_{i1}, a_{i2}, ..., a_{in}$($0 \leq a_{ij} \leq 50$)。保证满足 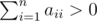。
输出格式
如果存在正整数 $k \geq 1$,使得矩阵 $a^k$ 是严格正的,输出 “YES” (不带引号)。否则输出 “NO” (不带引号)。
说明/提示
由 ChatGPT 5 翻译