CF405C Unusual Product

Little Chris is a huge fan of linear algebra. This time he has been given a homework about the unusual square of a square matrix. The dot product of two integer number vectors $ x $ and $ y $ of size $ n $ is the sum of the products of the corresponding components of the vectors. The unusual square of an $ n×n $ square matrix $ A $ is defined as the sum of $ n $ dot products. The $ i $ -th of them is the dot product of the $ i $ -th row vector and the $ i $ -th column vector in the matrix $ A $ . Fortunately for Chris, he has to work only in $ GF(2) $ ! This means that all operations (addition, multiplication) are calculated modulo 2. In fact, the matrix $ A $ is binary: each element of $ A $ is either 0 or 1. 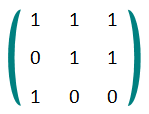For example, consider the following matrix $ A $ : The unusual square of $ A $ is equal to $ (1·1+1·0+1·1)+(0·1+1·1+1·0)+(1·1+0·1+0·0)=0+1+1=0 $ . However, there is much more to the homework. Chris has to process $ q $ queries; each query can be one of the following: 1. given a row index $ i $ , flip all the values in the $ i $ -th row in $ A $ ; 2. given a column index $ i $ , flip all the values in the $ i $ -th column in $ A $ ; 3. find the unusual square of $ A $ . To flip a bit value $ w $ means to change it to $ 1-w $ , i.e., 1 changes to 0 and 0 changes to 1. Given the initial matrix $ A $ , output the answers for each query of the third type! Can you solve Chris's homework?

The first line of input contains an integer $ n $ ( $ 1

Let the number of the 3rd type queries in the input be $ m $ . Output a single string $ s $ of length $ m $ , where the $ i $ -th symbol of $ s $ is the value of the unusual square of $ A $ for the $ i $ -th query of the 3rd type as it appears in the input.