CF405C Unusual Product

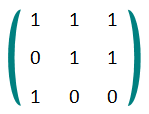
小 Chris 是线性代数的超级粉丝。这一次，他收到了一个关于方阵“特殊平方”的作业。 给定两个长度为 $n$ 的整数向量 $x$ 和 $y$，它们的点积是对应分量相乘后求和的结果。一个 $n \times n$ 的方阵 $A$ 的“特殊平方”被定义为 $n$ 个点积的和。第 $i$ 个点积是矩阵 $A$ 的第 $i$ 行向量与第 $i$ 列向量的点积。 幸运的是，Chris 只需要在 $GF(2)$ 域内操作！也就是说，所有的运算（加法、乘法）都模 $2$ 计算。实际上，矩阵 $A$ 是一个二进制矩阵：每个元素非零即一。例如，考虑如下矩阵 $A$：  $A$ 的“特殊平方”等于 $$(1\cdot1+1\cdot0+1\cdot1)+(0\cdot1+1\cdot1+1\cdot0)+(1\cdot1+0\cdot1+0\cdot0)=0+1+1=0。$$ 不过，作业还没完。Chris 还要处理 $q$ 个操作请求，每个请求可以是以下三种之一： 1. 给定行下标 $i$，翻转 $A$ 的第 $i$ 行的所有值； 2. 给定列下标 $i$，翻转 $A$ 的第 $i$ 列的所有值； 3. 查询 $A$ 的特殊平方。 翻转某个比特值 $w$ 意味着把它变成 $1-w$，即 $1$ 变为 $0$，$0$ 变为 $1$。 给定初始矩阵 $A$，对于每个第三种类型的查询，输出对应答案！你能帮 Chris 完成作业吗？

输入的第一行包含一个整数 $n$（$1 \leq n \leq 1000$），表示矩阵 $A$ 的行数和列数。接下来的 $n$ 行描述矩阵，每行包含 $n$ 个用空格分隔的 $0$ 或 $1$，表示第 $i$ 行。第 $i$ 行第 $j$ 个数 $a_{ij}$（$0 \leq a_{ij} \leq 1$）表示 $A$ 的第 $i$ 行第 $j$ 列的元素。 接下来的第 $n+1$ 行包含一个整数 $q$（$1 \leq q \leq 10^6$），表示操作请求的数量。接下来的 $q$ 行每行描述一个操作，具体如下： - 1 $i$ — 翻转第 $i$ 行（$1 \leq i \leq n$）； - 2 $i$ — 翻转第 $i$ 列（$1 \leq i \leq n$）； - 3 — 输出矩阵的特殊平方。 注意：由于输入输出的数据量可能非常大，不要在你的代码里使用慢速的输出方式。例如，在 C++ 中不要用 cin、cout。

假设输入中有 $m$ 个第 $3$ 种类型的查询。输出一个长度为 $m$ 的字符串 $s$，其中第 $i$ 个字符代表第 $i$ 个按顺序出现的类型 $3$ 查询的特殊平方结果。

由 ChatGPT 5 翻译