CF405D Toy Sum

Little Chris is very keen on his toy blocks. His teacher, however, wants Chris to solve more problems, so he decided to play a trick on Chris. There are exactly $ s $ blocks in Chris's set, each block has a unique number from 1 to $ s $ . Chris's teacher picks a subset of blocks $ X $ and keeps it to himself. He will give them back only if Chris can pick such a non-empty subset $ Y $ from the remaining blocks, that the equality holds: 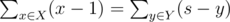 "Are you kidding me?", asks Chris.For example, consider a case where $ s=8 $ and Chris's teacher took the blocks with numbers 1, 4 and 5. One way for Chris to choose a set is to pick the blocks with numbers 3 and 6, see figure. Then the required sums would be equal: $ (1-1)+(4-1)+(5-1)=(8-3)+(8-6)=7 $ . However, now Chris has exactly $ s=10^{6} $ blocks. Given the set $ X $ of blocks his teacher chooses, help Chris to find the required set $ Y $ !

The first line of input contains a single integer $ n $ ( $ 1

In the first line of output print a single integer $ m $ ( $ 1