CF405E Graph Cutting

小 Chris 正在参加一个图切分比赛。他很专业。现在是考验他全部技能的时候了。 Chris 得到了一张简单的无向连通图，该图有 $n$ 个顶点（编号从 $1$ 到 $n$）和 $m$ 条边。问题是要将该图切分为长度为 $2$ 的不重复边路径。也就是说，需要将所有边划分成若干对，使得每一对中的两条边是相邻的，并且每条边只能属于一对。 例如，下图展示了一种对图进行切分的方式。第一个样例测试就包含了该图的描述。 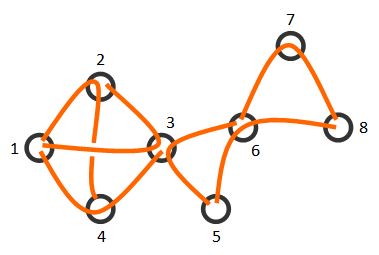 你有机会和 Chris 竞争。请找到一种切分当前图的方法，或者判断它是否不可能做到！

输入的第一行包含两个用空格分隔的整数 $n$ 和 $m$（$1 \leq n, m \leq 10^5$），分别表示图的顶点数和边数。接下来的 $m$ 行描述图中的边。第 $i$ 行包含两个用空格分隔的整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq n$；$a_i \neq b_i$），表示第 $i$ 条边连接 $a_i$ 和 $b_i$ 这两个顶点。保证给定的图是简单图（无自环和重边）且连通。 注意：由于输入、输出数据量可能非常大，禁止使用较慢的输出方式。例如，在 C++ 中不要使用 cin、cout。

如果可以将给定图切分为长度为 $2$ 的不重复边路径，则输出 $\frac{m}{2}$ 行，每行包含三个用空格分隔的整数 $x_i$、$y_i$ 和 $z_i$，表示第 $i$ 条路径。图中应包含该路径，即应包含 $(x_i, y_i)$ 和 $(y_i, z_i)$ 这两条边。每条边必须且只能出现在一条长度为 $2$ 的路径中。若存在多种切分方案，可以输出任意一种。 如果无法切分，则输出“No solution”（不带引号）。

由 ChatGPT 5 翻译